-
![Marrons Papéis de Parede]()
Marrons Wallpapers -
![Árvore De Natal Papéis de Parede]()
Árvore De Natal Wallpapers -
![Gamer Papéis de Parede]()
Gamer Wallpapers -
![Maquiagem Papéis de Parede]()
Maquiagem Wallpapers -
![Leitoso Papéis de Parede]()
Leitoso Wallpapers -
![No Man's Sky Papéis de Parede]()
No Man's Sky Wallpapers -
![Sol Papéis de Parede]()
Sol Wallpapers -
![Ano Novo Papéis de Parede]()
Ano Novo Wallpapers -
![Abacaxi Papéis de Parede]()
Abacaxi Wallpapers -
![Buda Papéis de Parede]()
Buda Wallpapers -
![Tóquio Papéis de Parede]()
Tóquio Wallpapers -
![Fevereiro Papéis de Parede]()
Fevereiro Wallpapers -
![Anônimo Papéis de Parede]()
Anônimo Wallpapers -
![São Petersburgo Papéis de Parede]()
São Petersburgo Wallpapers -
![Los Angeles Papéis de Parede]()
Los Angeles Wallpapers -
![Neve Papéis de Parede]()
Neve Wallpapers -
![Buraco Negro Papéis de Parede]()
Buraco Negro Wallpapers -
![Islândia Papéis de Parede]()
Islândia Wallpapers -
![Teclado Papéis de Parede]()
Teclado Wallpapers -
![Odsonne Édouard Papéis de Parede]()
Odsonne Édouard Wallpapers -
![Harley Davidson Papéis de Parede]()
Harley Davidson Wallpapers -
![Afeganistão Papéis de Parede]()
Afeganistão Wallpapers -
![Painel Papéis de Parede]()
Painel Wallpapers -
![Morrer Papéis de Parede]()
Morrer Wallpapers -
![Krishna 3d Papéis de Parede]()
Krishna 3d Wallpapers -
![Reis Do Sacramento Papéis de Parede]()
Reis Do Sacramento Wallpapers -
![Harrison Barnes Papéis de Parede]()
Harrison Barnes Wallpapers -
![Ipad Azul Papéis de Parede]()
Ipad Azul Wallpapers -
![Estética Todoroki Papéis de Parede]()
Estética Todoroki Wallpapers -
![Verde Da Floresta Papéis de Parede]()
Verde Da Floresta Wallpapers -
![Codificando Iphone Papéis de Parede]()
Codificando Iphone Wallpapers -
![Belo Pôr Do Sol Papéis de Parede]()
Belo Pôr Do Sol Wallpapers -
![Arjun Rampal Papéis de Parede]()
Arjun Rampal Wallpapers -
![Bratz Papéis de Parede]()
Bratz Wallpapers -
![Turtle Iphone Hd Papéis de Parede]()
Turtle Iphone Hd Wallpapers -
![Jarvis Papéis de Parede]()
Jarvis Wallpapers -
![Fukuoka Papéis de Parede]()
Fukuoka Wallpapers -
![Lee Moriarty Papéis de Parede]()
Lee Moriarty Wallpapers -
![Nova York Papéis de Parede]()
Nova York Wallpapers -
![Laptop Rosa Papéis de Parede]()
Laptop Rosa Wallpapers -
![Shih Tzu Papéis de Parede]()
Shih Tzu Wallpapers -
![Estética Gryffindor Papéis de Parede]()
Estética Gryffindor Wallpapers -
![Rastreamento Usps Papéis de Parede]()
Rastreamento Usps Wallpapers -
![Tela Inicial Do Iphone Papéis de Parede]()
Tela Inicial Do Iphone Wallpapers -
![Estética Moderna Papéis de Parede]()
Estética Moderna Wallpapers -
![Plano De Fundo Do Iphone Xs Max For Honor]()
Plano De Fundo Do Iphone Xs Max For Honor -
![Jedi Papéis de Parede]()
Jedi Wallpapers -
![Estética De Verão Papéis de Parede]()
Estética De Verão Wallpapers -
![Estrelas Fofas Papéis de Parede]()
Estrelas Fofas Wallpapers -
![Mangá Sasuke Papéis de Parede]()
Mangá Sasuke Wallpapers -
![Dope Ps4 Papéis de Parede]()
Dope Ps4 Wallpapers -
![Política Cristã Papéis de Parede]()
Política Cristã Wallpapers -
![Máscara De Purga Papéis de Parede]()
Máscara De Purga Wallpapers -
![Sinais Estéticos De Néon Grunge Papéis de Parede]()
Sinais Estéticos De Néon Grunge Wallpapers -
![John Klingberg Papéis de Parede]()
John Klingberg Wallpapers -
![Iphone Do Dallas Cowboys Papéis de Parede]()
Iphone Do Dallas Cowboys Wallpapers -
![Portal Iphone Papéis de Parede]()
Portal Iphone Wallpapers -
![Corra Papéis de Parede]()
Corra Wallpapers -
![Flamengo Papéis de Parede]()
Flamengo Wallpapers -
![Gabriel Jesus Papéis de Parede]()
Gabriel Jesus Wallpapers -
![Floral Verde Papéis de Parede]()
Floral Verde Wallpapers -
![Médico Dorme Papéis de Parede]()
Médico Dorme Wallpapers -
![Ipad Kawaii Fofo Papéis de Parede]()
Ipad Kawaii Fofo Wallpapers -
![Spirited Away Minimalista Papéis de Parede]()
Spirited Away Minimalista Wallpapers -
![Tupac Papéis de Parede]()
Tupac Wallpapers -
![Kevin Owens Papéis de Parede]()
Kevin Owens Wallpapers -
![La La Land 4k Papéis de Parede]()
La La Land 4k Wallpapers -
![Kevin Hart Papéis de Parede]()
Kevin Hart Wallpapers -
![Saúde Mental Papéis de Parede]()
Saúde Mental Wallpapers -
![Cérbero Papéis de Parede]()
Cérbero Wallpapers -
![Aeroflot Papéis de Parede]()
Aeroflot Wallpapers -
![Motivação Financeira Papéis de Parede]()
Motivação Financeira Wallpapers -
![Hyuga Papéis de Parede]()
Hyuga Wallpapers -
![Capturas De Tela Papéis de Parede]()
Capturas De Tela Wallpapers -
![Julie Papéis de Parede]()
Julie Wallpapers -
![Fundo Do Pixel 3 Da Califórnia]()
Fundo Do Pixel 3 Da Califórnia -
![Gru Papéis de Parede]()
Gru Wallpapers -
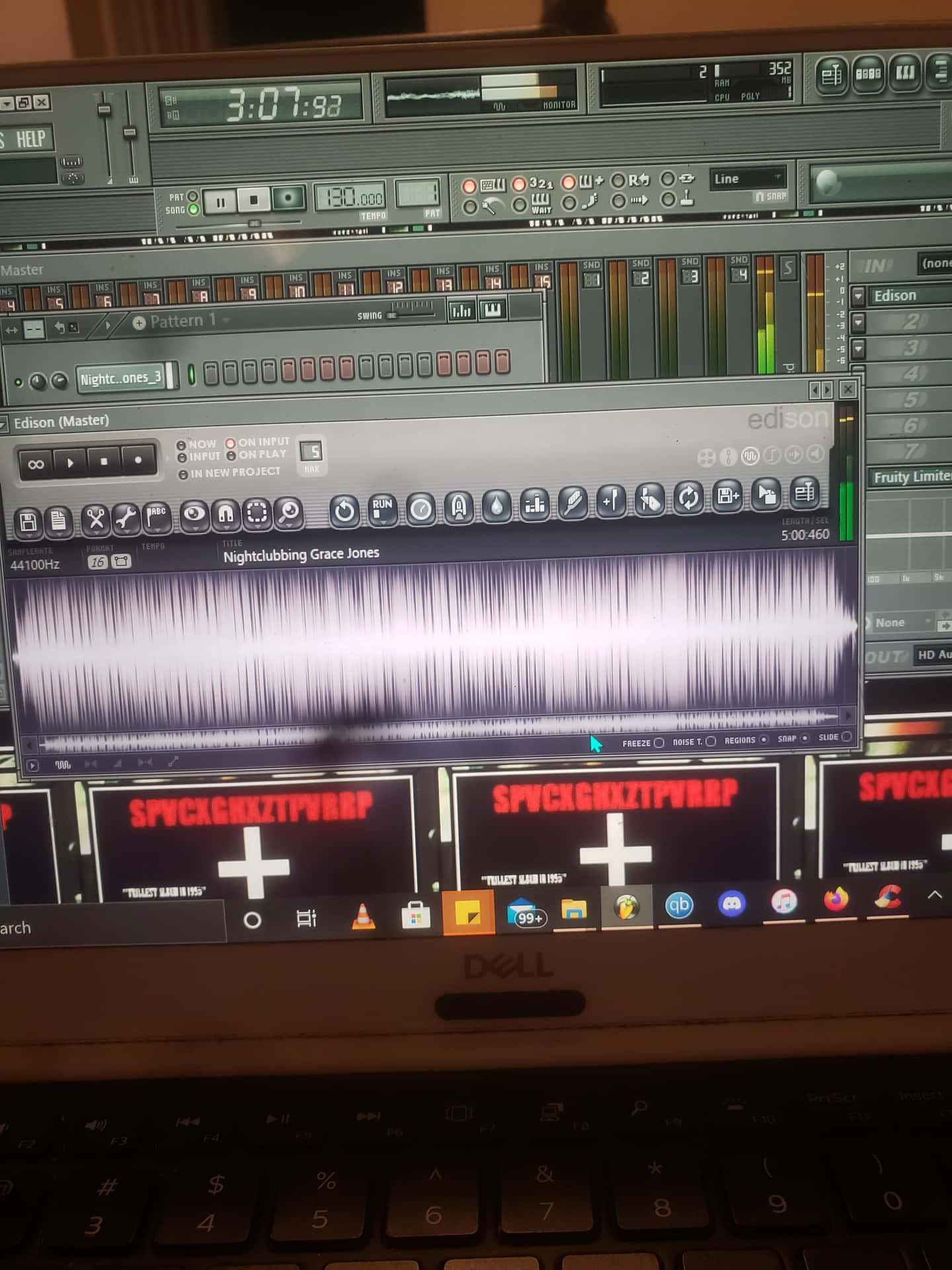
![Estúdio Fl Papéis de Parede]()
Estúdio Fl Wallpapers -
![Ravindra Jadeja Papéis de Parede]()
Ravindra Jadeja Wallpapers -
![Mercedes F1 Iphone Papéis de Parede]()
Mercedes F1 Iphone Wallpapers -
![Futebol De Auburn Papéis de Parede]()
Futebol De Auburn Wallpapers -
![Desenho Animado De Shiva Papéis de Parede]()
Desenho Animado De Shiva Wallpapers -
![O Bom Dinossauro Papéis de Parede]()
O Bom Dinossauro Wallpapers -
![Sano Papéis de Parede]()
Sano Wallpapers -
![Porter Airlines Papéis de Parede]()
Porter Airlines Wallpapers -
![Fundo Roxo De Halloween]()
Fundo Roxo De Halloween -
![Estética Bonita Papéis de Parede]()
Estética Bonita Wallpapers -
![Vespas Papéis de Parede]()
Vespas Wallpapers -
![Máquinas Papéis de Parede]()
Máquinas Wallpapers -
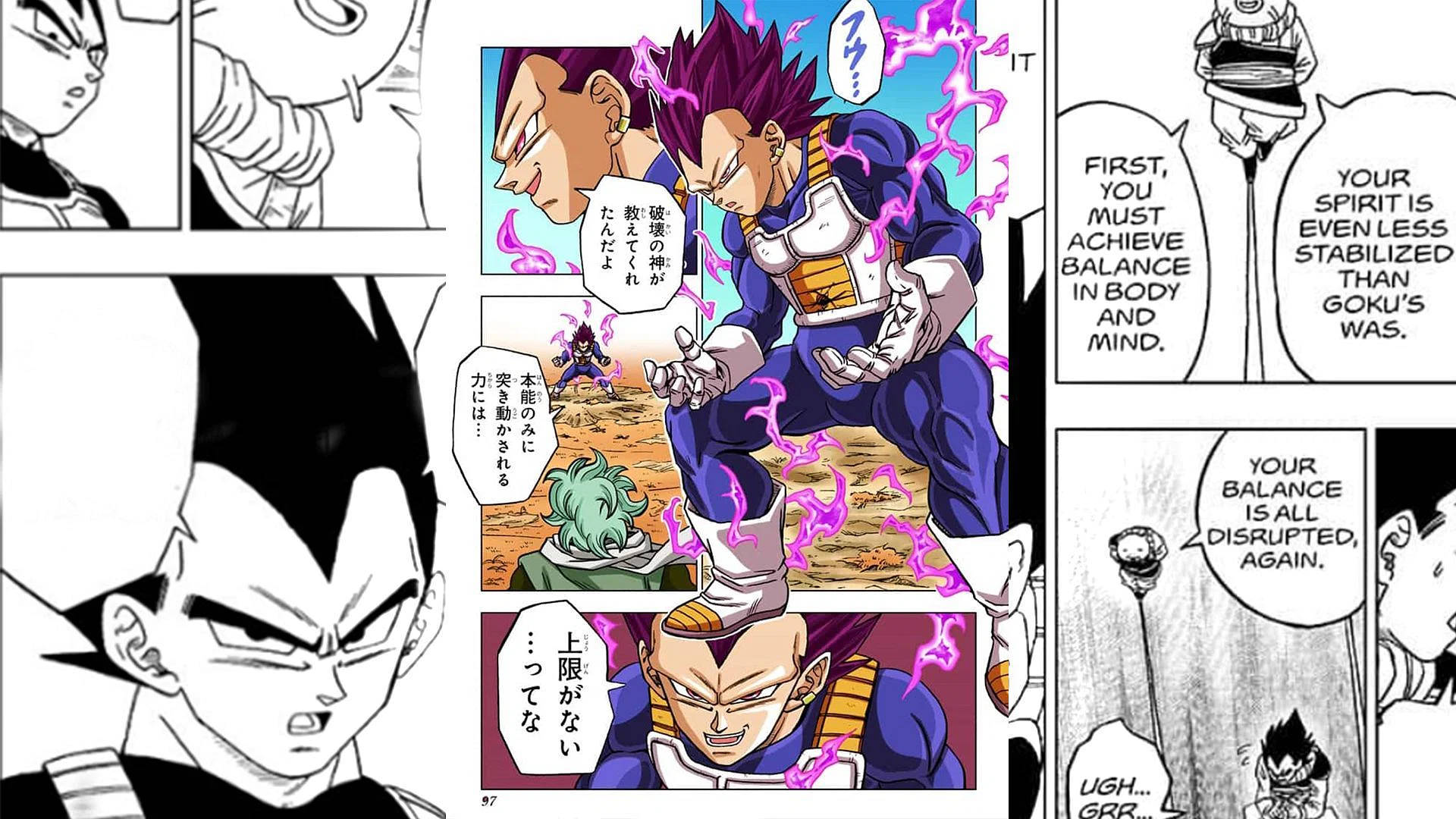
![Dragon Ball Super Papéis de Parede]()
Dragon Ball Super Wallpapers -
![Sean Penn Papéis de Parede]()
Sean Penn Wallpapers -
![Estética Rosa Neon Papéis de Parede]()
Estética Rosa Neon Wallpapers -
![Verde Minimalista Papéis de Parede]()
Verde Minimalista Wallpapers -
![Bette Davis Papéis de Parede]()
Bette Davis Wallpapers -
![Iphone Rosa Preta Papéis de Parede]()
Iphone Rosa Preta Wallpapers -
![Oslo Papéis de Parede]()
Oslo Wallpapers -
![Papel De Parede Para Celular Gratis Monstera]()
Papel De Parede Para Celular Gratis Monstera -
![Jonathan Osório Papéis de Parede]()
Jonathan Osório Wallpapers -
![O Falcão E O Soldado Do Inverno Papéis de Parede]()
O Falcão E O Soldado Do Inverno Wallpapers -
![Fundo Rosa E Azul]()
Fundo Rosa E Azul -
![Rurouni Papéis de Parede]()
Rurouni Wallpapers -
![Basquete Preto Papéis de Parede]()
Basquete Preto Wallpapers -
![Localização De Five Nights At Freddy's Sister Papéis de Parede]()
Localização De Five Nights At Freddy's Sister Wallpapers -
![Ralph Quebra A Internet Papéis de Parede]()
Ralph Quebra A Internet Wallpapers -
![Agora Unidos Papéis de Parede]()
Agora Unidos Wallpapers -
![Dubai 4k Papéis de Parede]()
Dubai 4k Wallpapers -
![Chadwick Boseman Papéis de Parede]()
Chadwick Boseman Wallpapers -
![Linda Costura De Bebê Papéis de Parede]()
Linda Costura De Bebê Wallpapers -
![Ojays Papéis de Parede]()
Ojays Wallpapers -
![Finais Da Nba Papéis de Parede]()
Finais Da Nba Wallpapers -
![Mount Vernon Papéis de Parede]()
Mount Vernon Wallpapers -
![Fundo Noturno]()
Fundo Noturno -
![Adoro O Computador Papéis de Parede]()
Adoro O Computador Wallpapers -
![Steven Adams Papéis de Parede]()
Steven Adams Wallpapers -
![Incrível Inverno Em 4k Papéis de Parede]()
Incrível Inverno Em 4k Wallpapers -
![Ralph Papéis de Parede]()
Ralph Wallpapers -
![Anime Cítrico Papéis de Parede]()
Anime Cítrico Wallpapers -
![Paul Mccartney E Asas Papéis de Parede]()
Paul Mccartney E Asas Wallpapers -
![Fundo Verde Menta]()
Fundo Verde Menta -
![Paisagem Polissaca Papéis de Parede]()
Paisagem Polissaca Wallpapers -
![Citações Sobre Leões Papéis de Parede]()
Citações Sobre Leões Wallpapers -
![Mcm Papéis de Parede]()
Mcm Wallpapers -
![Swami Papéis de Parede]()
Swami Wallpapers -
![Montanha-russa Papéis de Parede]()
Montanha-russa Wallpapers -
![Leitelho Papéis de Parede]()
Leitelho Wallpapers -
![Rockruff Papéis de Parede]()
Rockruff Wallpapers -
![Noite Escura Papéis de Parede]()
Noite Escura Wallpapers -
![Jolteon Papéis de Parede]()
Jolteon Wallpapers -
![Revirar Os Olhos Papéis de Parede]()
Revirar Os Olhos Wallpapers -
![Lance Storm Papéis de Parede]()
Lance Storm Wallpapers -
![Jogo Tomb Raider Papéis de Parede]()
Jogo Tomb Raider Wallpapers -
![Livre Papéis de Parede]()
Livre Wallpapers -
![Joji Papéis de Parede]()
Joji Wallpapers -
![Código Iphone Papéis de Parede]()
Código Iphone Wallpapers -
![Playboy Papéis de Parede]()
Playboy Wallpapers -
![Prado Papéis de Parede]()
Prado Wallpapers -
![Verde Néon Papéis de Parede]()
Verde Néon Wallpapers -
![Kenneth Branagh Papéis de Parede]()
Kenneth Branagh Wallpapers -
![Fundo De Fotografia De Alimentos]()
Fundo De Fotografia De Alimentos -
![Fundo Da Mesa De Alimentos]()
Fundo Da Mesa De Alimentos -
![Cidade Do Cabo Papéis de Parede]()
Cidade Do Cabo Wallpapers -
![James Storm Papéis de Parede]()
James Storm Wallpapers -
![Bavaria Papéis de Parede]()
Bavaria Wallpapers -
![Matador De Demônios Negros Papéis de Parede]()
Matador De Demônios Negros Wallpapers -
![Paranormal Papéis de Parede]()
Paranormal Wallpapers -
![Chevron Iphone Papéis de Parede]()
Chevron Iphone Wallpapers -
![Estética Sparkle Papéis de Parede]()
Estética Sparkle Wallpapers -
![Xadrez Papéis de Parede]()
Xadrez Wallpapers -
![Iphone De Designer Papéis de Parede]()
Iphone De Designer Wallpapers -
![Equitação Em Touro Papéis de Parede]()
Equitação Em Touro Wallpapers -
![Forte Mehrangarh Papéis de Parede]()
Forte Mehrangarh Wallpapers -
![Lindo Dragão Papéis de Parede]()
Lindo Dragão Wallpapers -
![Logotipo Valorant Papéis de Parede]()
Logotipo Valorant Wallpapers -
![Flor Fofa Para Iphone Papéis de Parede]()
Flor Fofa Para Iphone Wallpapers -
![Desktop Velozes E Furiosos Papéis de Parede]()
Desktop Velozes E Furiosos Wallpapers -
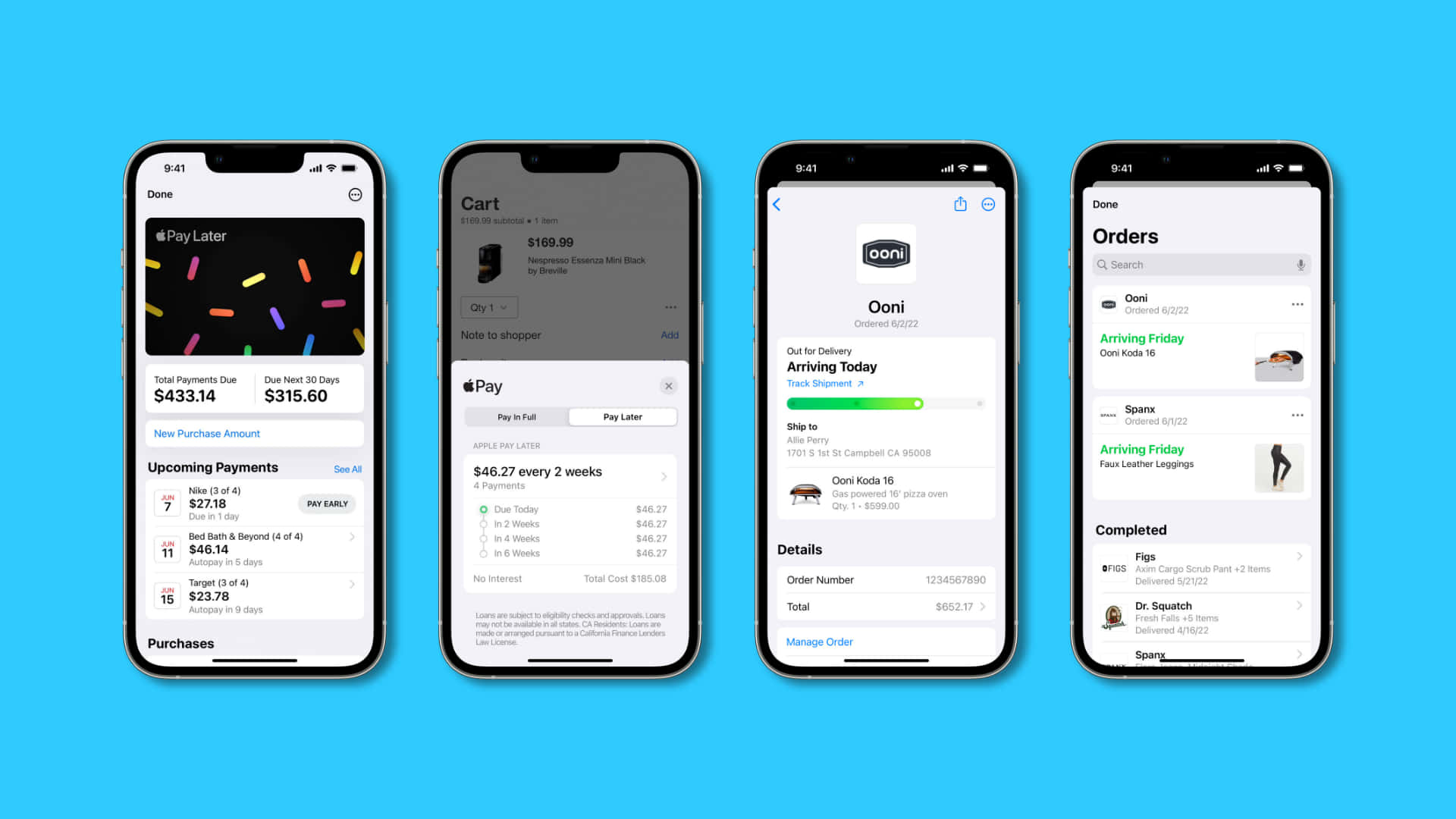
![Apple Pay Papéis de Parede]()
Apple Pay Wallpapers -
![George Russell Papéis de Parede]()
George Russell Wallpapers -
![Espectro Papéis de Parede]()
Espectro Wallpapers -
![Poodle Papéis de Parede]()
Poodle Wallpapers -
![Apenas Faça Papéis de Parede]()
Apenas Faça Wallpapers -
![Bryce Dallas Howard Papéis de Parede]()
Bryce Dallas Howard Wallpapers -
![Bmw Android Papéis de Parede]()
Bmw Android Wallpapers -
![Coringa Perigoso Papéis de Parede]()
Coringa Perigoso Wallpapers -
![Masha E O Urso Papéis de Parede]()
Masha E O Urso Wallpapers -
![Harrison Ford Papéis de Parede]()
Harrison Ford Wallpapers -
![Misa Papéis de Parede]()
Misa Wallpapers -
![Nba Papéis de Parede]()
Nba Wallpapers -
![Among Us Red Papéis de Parede]()
Among Us Red Wallpapers -
![Anime De Halloween Papéis de Parede]()
Anime De Halloween Wallpapers -
![Absol Papéis de Parede]()
Absol Wallpapers -
![Roupa Supreme Dos Desenhos Animados Papéis de Parede]()
Roupa Supreme Dos Desenhos Animados Wallpapers -
![Papel De Parede Para Celular Gratis Dwayne Johnson]()
Papel De Parede Para Celular Gratis Dwayne Johnson -
![Cr7 Papéis de Parede]()
Cr7 Wallpapers -
![Encosta Papéis de Parede]()
Encosta Wallpapers -
![Monterey Papéis de Parede]()
Monterey Wallpapers -
![David Nalbandian Papéis de Parede]()
David Nalbandian Wallpapers -
![Tiro Papéis de Parede]()
Tiro Wallpapers -
![Canguru Papéis de Parede]()
Canguru Wallpapers -
![Fenda Selvagem Papéis de Parede]()
Fenda Selvagem Wallpapers -
![Vigias Papéis de Parede]()
Vigias Wallpapers -
![Papel De Parede Para Celular Gratis Miles Morales Iphone]()
Papel De Parede Para Celular Gratis Miles Morales Iphone -
![Super Meat Boy Papéis de Parede]()
Super Meat Boy Wallpapers -
![Mãe Legal Papéis de Parede]()
Mãe Legal Wallpapers -
![Anel De Casamento Papéis de Parede]()
Anel De Casamento Wallpapers -
![Bebê Fofo Papéis de Parede]()
Bebê Fofo Wallpapers -
![Janelas Escuras Papéis de Parede]()
Janelas Escuras Wallpapers -
![Eric Cantona Papéis de Parede]()
Eric Cantona Wallpapers -
![Preppy Roblox Papéis de Parede]()
Preppy Roblox Wallpapers -
![Preto E Roxo Papéis de Parede]()
Preto E Roxo Wallpapers -
![Pulseira De Ferramentas Papéis de Parede]()
Pulseira De Ferramentas Wallpapers -
![Batata Doce Papéis de Parede]()
Batata Doce Wallpapers -
![Roma 2 Papéis de Parede]()
Roma 2 Wallpapers -
![Nihilus Da Terra Papéis de Parede]()
Nihilus Da Terra Wallpapers -
![Robert Vaughn Papéis de Parede]()
Robert Vaughn Wallpapers -
![Knuckles, A Equidna Papéis de Parede]()
Knuckles, A Equidna Wallpapers -
![Amo Um Casal Fofo Papéis de Parede]()
Amo Um Casal Fofo Wallpapers -
![Jai Shri Ram Papéis de Parede]()
Jai Shri Ram Wallpapers -
![Bruce Lee Papéis de Parede]()
Bruce Lee Wallpapers -
![Antigo Natal Estético Papéis de Parede]()
Antigo Natal Estético Wallpapers -
![Simone Biles Papéis de Parede]()
Simone Biles Wallpapers - Próxima página
Search